7 생물학적 동등성

생물학적동등성시험(bioequivalence test)는 기존 의약품의 특허가 만료된 후, 해당 의약품을 동일하게 개발하여 판매하고자 할 때 수행하는 임상시험이다. [1] 기존 오리지날 의약품(Reference)과 새로 개발한 의약품 즉 시험약(Test)을 교차연구(crossover study)의 형태로 투여한 뒤, 혈중 농도로부터 구한 약동학적 파라미터(pharmacokinetic parameter) 를 비교하여 평가하게 된다. 비교평가항목은 검체가 혈액인 경우, 1회 투약 시 AUCt, Cmax, 반복투약 시 AUCτ, Css,max를 주로 사용한다. 다만, 니트로글리세린 설하정과 같이 빠른 약효를 나타내는 제제 등은 Tmax를 비교평가항목으로 추가하기도 한다.

약동학 파라미터는 로그정규분포(log-normal distribution)을 따르고, 대조약과 시험약의 산출된 곡선하 면적(AUC)과 최대 농도 Cmax의 geometric mean ratio가 0.8 ~ 1.25 이내일 때, 약동학적으로 동등하다고 평가하게 된다. [2]

생물학적 동등성을 평가하는데 통계학은 핵심적인 역할을 수행하고 있고, 통계적 분석을 위해서는 컴퓨터 소프트웨어가 필요하다. SAS, SPSS 등과 같은 통계처리 프로그램을 혹은 독자 개발된 프로그램으로 통계적 검정을 실시할 수 있다. [3]

그러나 각각의 소프트웨어가 사용하기 어렵고 과정이 복잡하며 큰 비용이 소모되었다. 특히 약동학 분석 초보자나 통계학 비전공자가 사용하기 어려웠다. 본 저자들은 EDISON 사이언스 앱, R 샤이니(Shiny) 앱을 사용하여 이 과정을 연속성을 지닌 한 과정으로 통합하였다. 본 연구가 제시하는 방법을 통해 쉽고 정확하고 비용이 들지 않는 빠른 비구획분석과 생물학적 동등성 분석이 가능하다는 것을 보이고자 한다.

생물학적 동등성을 위한 가장 간단한 방법은 BE 패키지(Bae 2018)를 쓰는 것입니다.

Chow와 Liu의 책의 내용을 충실히 반영하였습니다. (Chow and Liu 2008) 생물학적 동등성을 위한 수학 식은 다음과 같습니다. (7.1)

\[\begin{equation} \begin{split} 0.8 < & 90\%\ CI\ of\ \frac{GM(AUC_{last, test})}{GM(AUC_{last, ref})} < 1.25 \\ 0.8 < & 90\%\ CI\ of\ \frac{GM(AUC_{last, test})}{GM(AUC_{last, ref})} < 1.25 \end{split} \tag{7.1} \end{equation}\]

현재로서는 2x2 디자인의 간단한 임상시험 디자인만을 지원하고 있습니다. (그림 7.1) 핵심이 되는 함수는 beNCA() 입니다.

knitr::include_graphics('images/twobytwo.jpg')
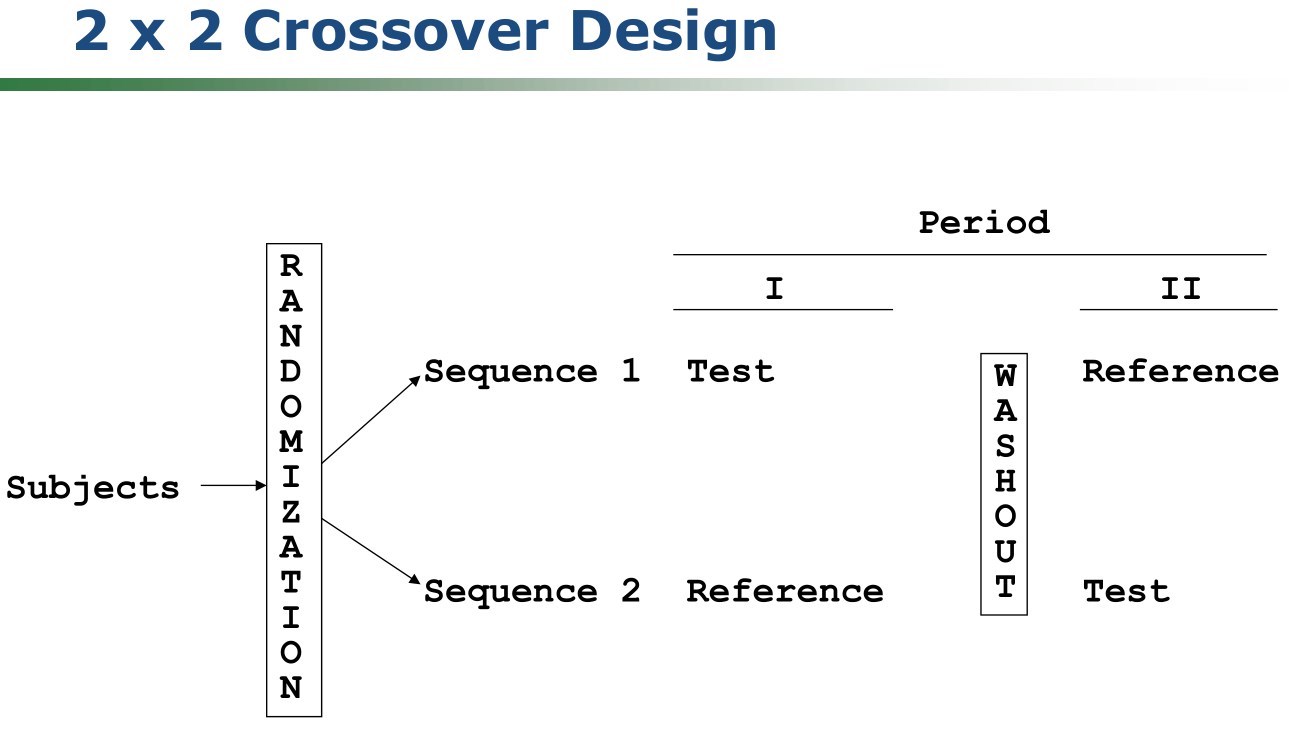
전형적인 2x2 설계

Figure 7.1: 전형적인 2x2 설계 

## function (Data, Columns = c("AUClast", "Cmax", "Tmax"), rtfName = "") 
## NULL

다음과 같은 함수 인자를 설정해 주면 됩니다.

  • SUBJ: Subject ID, any data type
  • GRP: column name in which information of “RT” or “TR” exists.
  • PRD: column name in which information of 1 or 2 exists.
  • TRT: column name in which information of “R” or “T” exists.
  • method: kbe by authors or nlme package uploaded on CRAN
Table 7.1: A example dataset for the bioequivalence test.
SUBJ GRP PRD TRT AUClast Cmax Tmax
1 RT 1 R 5018.927 1043.13 1.04
1 RT 2 T 6737.507 894.21 1.03
2 TR 1 T 4373.970 447.26 1.01
2 TR 2 R 6164.276 783.92 1.98
4 TR 1 T 5592.993 824.42 1.97
4 TR 2 R 5958.160 646.31 0.97

BE 패키지에 내장되어 있는 자료인 NCAResult4BE를 사용하겠습니다. (표 7.1) 33명의 대상자에 대해 2x2 교차설계 임상시험의 약동학 파라미터 AUClast, Cmax, Tmax 자료가 정리되어 있습니다.

print(be2x2(NCAResult4BE, c("AUClast", "Cmax", "Tmax")), na.print="") 
## $AUClast
## $AUClast$`Analysis of Variance (log scale)`
##                          SS DF           MS           F            p
## SUBJECT        2.875497e+00 32 8.985928e-02 3.183942248 0.0008742828
## GROUP          1.024607e-01  1 1.024607e-01 1.145416548 0.2927731856
## SUBJECT(GROUP) 2.773036e+00 31 8.945279e-02 3.169539016 0.0009544080
## PERIOD         3.027399e-05  1 3.027399e-05 0.001072684 0.9740824428
## DRUG           3.643467e-02  1 3.643467e-02 1.290972690 0.2645764201
## ERROR          8.749021e-01 31 2.822265e-02                         
## TOTAL          3.786834e+00 65                                      
## 
## $AUClast$`Between and Within Subject Variability`
##                                 Between Subject Within Subject
## Variance Estimate                    0.03061507     0.02822265
## Coefficient of Variation, CV(%)     17.63193968    16.91883011
## 
## $AUClast$`Least Square Means (geometric mean)`
##                 Reference Drug Test Drug
## Geometric Means       5092.098  4858.245
## 
## $AUClast$`90% Confidence Interval of Geometric Mean Ratio (T/R)`
##                  Lower Limit Point Estimate Upper Limit
## 90% CI for Ratio    0.889436      0.9540753    1.023412
## 
## $AUClast$`Sample Size`
##                       True Ratio=1 True Ratio=Point Estimate
## 80% Power Sample Size            6                         7
## 
## 
## $Cmax
## $Cmax$`Analysis of Variance (log scale)`
##                          SS DF           MS           F          p
## SUBJECT        2.861492e+00 32 8.942162e-02 2.237604579 0.01367095
## GROUP          9.735789e-05  1 9.735789e-05 0.001054764 0.97429977
## SUBJECT(GROUP) 2.861394e+00 31 9.230304e-02 2.309706785 0.01131826
## PERIOD         4.717497e-03  1 4.717497e-03 0.118046317 0.73348258
## DRUG           6.837756e-03  1 6.837756e-03 0.171101730 0.68198228
## ERROR          1.238856e+00 31 3.996310e-02                       
## TOTAL          4.112258e+00 65                                    
## 
## $Cmax$`Between and Within Subject Variability`
##                                 Between Subject Within Subject
## Variance Estimate                    0.02616997      0.0399631
## Coefficient of Variation, CV(%)     16.28355371     20.1921690
## 
## $Cmax$`Least Square Means (geometric mean)`
##                 Reference Drug Test Drug
## Geometric Means       825.5206  808.8778
## 
## $Cmax$`90% Confidence Interval of Geometric Mean Ratio (T/R)`
##                  Lower Limit Point Estimate Upper Limit
## 90% CI for Ratio   0.9013625      0.9798396    1.065149
## 
## $Cmax$`Sample Size`
##                       True Ratio=1 True Ratio=Point Estimate
## 80% Power Sample Size            8                         8
## 
## 
## $Tmax
## $Tmax$`Wilcoxon Signed-Rank Test`
##   p-value 
## 0.2326894 
## 
## $Tmax$`Hodges-Lehmann Estimate`
##                            Lower Limit Point Estimate Upper Limit
## 90% Confidence Interval       -0.33000       -0.03500      0.1050
## 90% Confidence Interval(%)    74.37661       97.28237    108.1529
knitr::include_graphics('images/fixed-random.jpg')
모수 인자와 변량 인자의 비교

Figure 7.2: 모수 인자와 변량 인자의 비교

7.1 이론 및 계산방법

7.1.1 EDISON 사이언스 앱, R 샤이니 앱과 R 패키지

본 분석에서 사용될 EDISON 사이언스 앱, R 샤이니 앱은 NonCompartEdison, edisonBE 두 종류이다. 비구획분석과 생물학적동등성 통계 분석을 하게 되며 R 기반 [4] 으로 프로그래밍 되어 있다. 각각은 NonCompart와 BE라는 이름의 R 패키지 형태로 공개되어 배포 되고 있다. R 콘솔에서는 다음을 입력함으로서 각 라이브러리를 불러올 수 있다.

install.packages("NonCompart")
install.packages("BE")
library(NonCompart)
library(BE)

EDISON 사이언스 앱, R 샤이니 앱을 제작하는데 사용한 R 코드 및 자료(datasets)는 https://github.com/asancpt/edison-noncompart, https://github.com/asancpt/edison-BE 에 각각 공개되어 있다.

7.1.2 모형

\[ Y_{ijk} = \mu + S_{ik} + P_{j} + F_{j,k} + C_{(j-1,k)} + \varepsilon_{ijk} \]

이때에 μ; 전체 평균, Sik; k 번째 sequence에서 i 번째 subject의 효과(랜덤), Pj : j번째 period 의 효과(고정), Fj, k; k 번째 sequence에서 j 번째 period의 제제의 효과(고정), C(j-1,k): k 번째 sequence에서(j-1) 번째 period의 잔류효과(고정), εijk : 오차항으로 정의한다. 이 모델에서 사용하는 가정은 1) Sik ∼ N(0,σs²), 2) εijk ∼ N(0,σe²), 3) Sik 와 εijk가 독립이라는 세가지 이다. 이때 (μT - μR)에 대한 (1-2α)×100% 신뢰구간이 ln(0.8), ln(1.25) 안에 들어가면 두제제가 생물학적으로 동등하다 결론을 내릴 수 있다.

7.1.3 SAS 코드

SAS는 통계 패키지중에서는 가장 방대하고 다양한 분석을 제공하고 전 세계적으로 생물학적동등성의 판단을 위해 표준으로 사용되고 있다. 다음과 같이 2x2 교차설계 자료를 분석하기 위한 SAS 코드 (PROC GLM, PROC MIXED, SAS version 9.4)를 작성하고 EDISON 사이언스 앱, R 샤이니 앱에서 계산된 결과와 비교하였다.

PROC GLM DATA=BE OUTSTAT=STATRES; /* GLM use only complete subjects. */
CLASS SEQ PRD TRT SUBJ;
MODEL LNAUCL = SEQ SUBJ(SEQ) PRD TRT;
RANDOM SUBJ(SEQ)/TEST;
LSMEANS TRT /PDIFF=CONTROL('R') CL ALPHA=0.1 COV OUT=LSOUT;

PROC MIXED DATA=BE; /* MIXED uses all data. */
CLASS SEQ TRT SUBJ PRD;
MODEL LNAUCL = SEQ PRD TRT;
RANDOM SUBJ(SEQ);
ESTIMATE 'T VS R' TRT -1 1 /CL ALPHA=0.1;
ODS OUTPUT ESTIMATES=ESTIM COVPARMS=COVPAR;

7.1.4 자료의 형태, 자료의 구성요소

2x2 cross-over design이 가장 기본적인 디자인(통상 RT / TR)으로 사용된다. 피험자를 무작위로 두 군으로 나누어 각 군별로 동일 성분의 대조약과 시험약을 각각 투여(제1기 투약)하고 피험자별로 투약 전후 정해진 시간마다 채혈하고 농도 측정한다. 이전에 투여한 약이 모두 배설될 정도로 충분한 기간 경과 (보통 반감기의 5배 이상) 후 각 군별로 대조약과 시험약을 바꾸어 각각 투여하고(제2기 투약) 동일하게 혈액 채취 및 혈중농도 측정하게 된다.

본 논문에서는 위와 같은 시나리오로 시뮬레이션을 통해 얻어진 약동학 파라미터를 사용해 자료가 구성되었고, EDISON 사이언스 앱인 NonCompartEdison에서 입력으로 사용될 자료의 형태는 Table 1와 같다. SEQ (sequence), TRT (treatment), SUBJ (subject), and PRD (period, 기)의 자료가 열 형태로 제시되어야 하며 이는 edisonBE 앱에서 사용되는 약동학 파라미터 자료에도 일종의 primary key로 사용되기 때문에 유사한 형태로 보존되어야 한다. 33명의 대상자의 개인별 농도-시간 그래프는 Figure 1에 나타내었다.

knitr::include_graphics("images/figure-conc-time-curve.png")
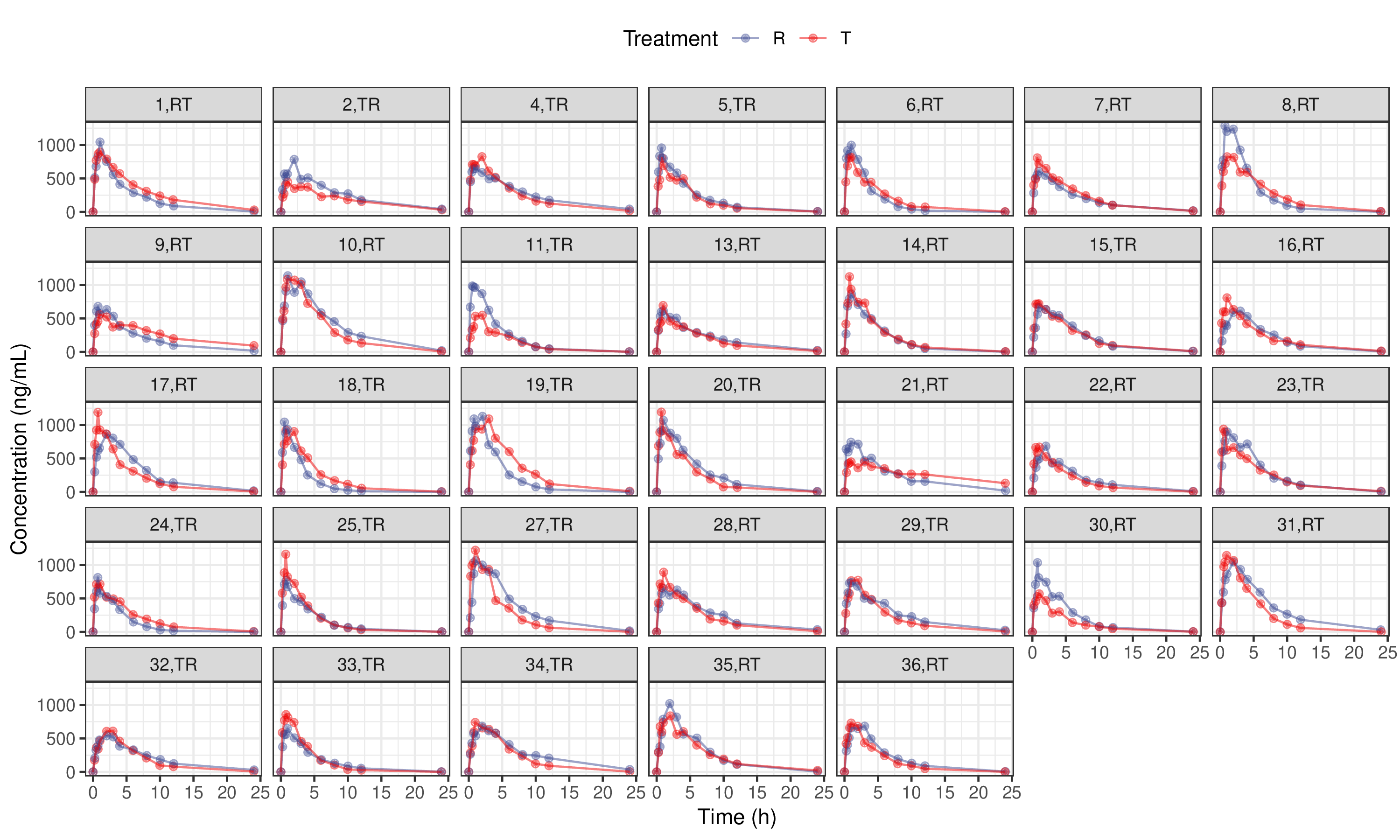
Concentration-time curves of raw data (N=33)

Figure 7.3: Concentration-time curves of raw data (N=33)

7.2 결과

7.2.1 NonCompartEdison 앱을 통한 비구획분석

Table 1. An example of the raw concentration-time data used for EDISON Science Apps. The dataset was simulated based on the 2x2 crossover design.

SUBJ GRP PRD TRT nTIME TIME CONC
1 RT 1 R 0 0 0
1 RT 1 R 0.25 0.26 511.3
1 RT 1 R 0.5 0.46 678.79
1 RT 1 R … … …
1 RT 2 T 0 0 0
1 RT 2 T 0.25 0.25 487.62
1 RT 2 T 0.5 0.48 769.6
… … … … … … …
5 TR 1 T 0 0 0
5 TR 1 T 0.25 0.23 382.79
5 TR 1 T 0.5 0.45 477.03
5 TR 1 T … … …
5 TR 2 R 0 0 0
5 TR 2 R 0.25 0.28 596.98
5 TR 2 R 0.5 0.47 832.76
5 TR 2 R … … …
… … … … … … …

농도-시간 입력 자료(Table 1)는 NonCompartEdison 앱을 통해서 처리되어 약동학 파라미터가 계산되어 표형태의 출력 자료가 된다. (Table 2) 이것이 다시 edisonBE 앱의 입력자료가 되어 생물학적동등성 분석을 위해 쓰이게 된다.

Table 2. The raw pharmacokinetic data calculated by NonCompartEdison App

SUBJ GRP PRD TRT AUClast Cmax Tmax
1 RT 1 R 5018.927 1043.13 1.04
1 RT 2 T 6737.507 894.21 1.03
2 TR 1 T 4373.97 447.26 1.01
2 TR 2 R 6164.276 783.92 1.98
4 TR 1 T 5592.993 824.42 1.97
4 TR 2 R 5958.16 646.31 0.97
5 TR 1 T 3902.59 803.7 0.8
5 TR 2 R 4620.156 955.3 0.74

7.2.2 edisonBE 앱을 통한 생물학적동등성 판단

약동학 파라미터가 입력 자료가 되어 edisonBE 앱을 통해 처리되고 생물학적동등성 판단을 위한 ANOVA 표, 변이 (variability), Least square mean (LSM), geometric mean ratio (GMR)의 90% 신뢰구간, 샘플 수의 계산이 수행된다. (Figure 2) 본 자료로 계산한 AUClast는 생물학적 동등성 기준을 만족하고 있다.

knitr::include_graphics("assets-paper/figure-2.png")
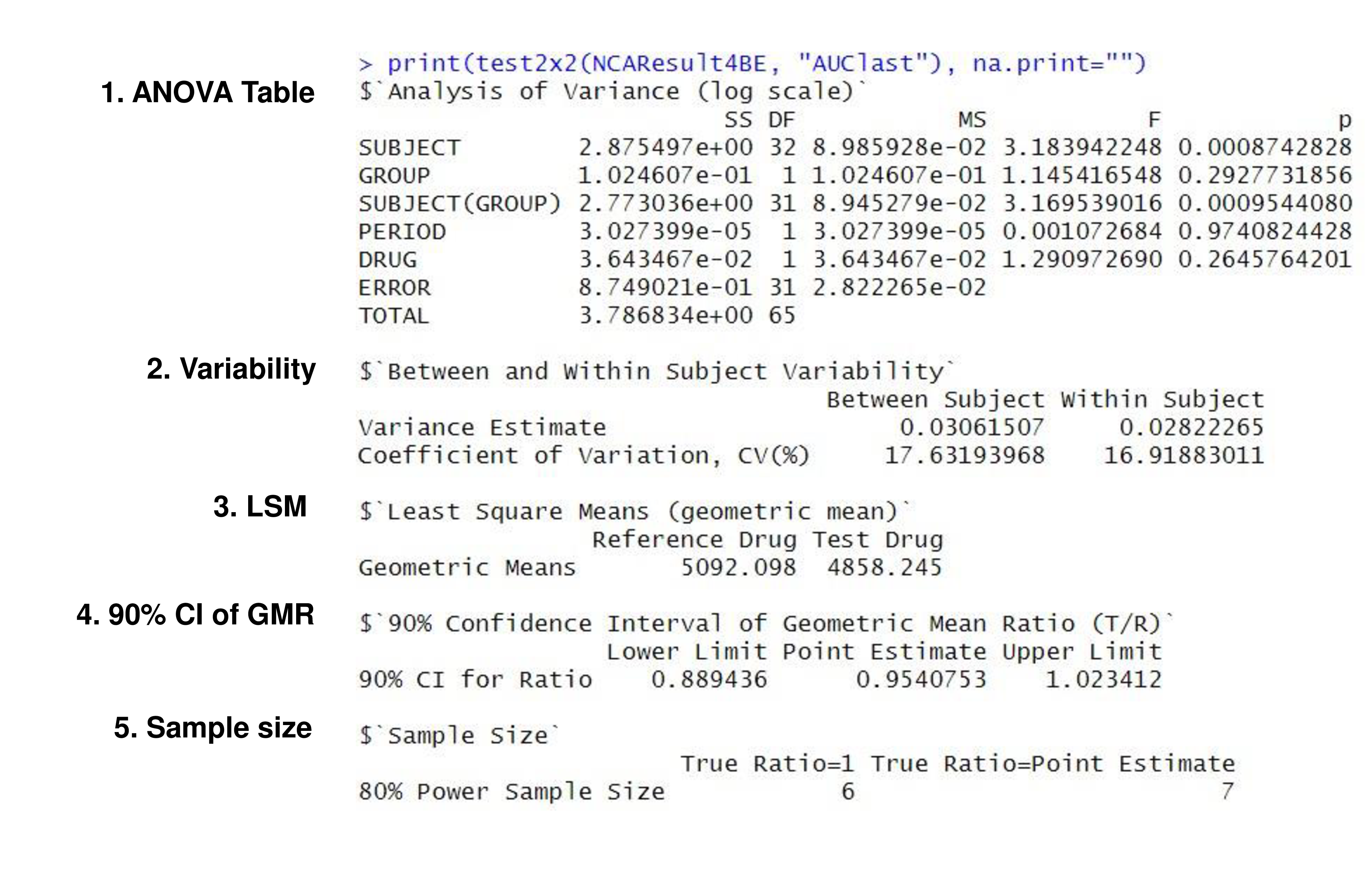
Output format of bioequivalence tests performed by BE R package.

Figure 7.4: Output format of bioequivalence tests performed by BE R package.

7.2.3 90% 신뢰구간의 SAS 결과값과 비교

위 과정으로 얻어진 계산값은 가장 정확하게 생물학적 동등성을 평가하고 있어 표준으로 사용되는SAS 소프트웨어 결과값과 완전히 동일하였다. (Table 3)

Table 3. Comparison of 90% confidence interval for the ratio of the geometric means of (A) AUClast and (B) Cmax

A

Analysis Lower Limit Point Estimate Upper Limit
EDISON Science App 0.88944 0.95408 1.02341
SAS: PROC GLM 0.88944 0.95408 1.02341
SAS: PROC MIXED 0.88944 0.95408 1.02341

B

Analysis Lower Limit Point Estimate Upper Limit
EDISON Science App 0.90136 0.97984 1.06515
SAS: PROC GLM 0.90136 0.97984 1.06515
SAS: PROC MIXED 0.90136 0.97984 1.06515

7.2.4 샘플 수 계산

BE 패키지를 통한 분석은 Between subject CV값과 Within Subject CV를 계산한다. 이에 근거하여 80%의 파워로 계산한 샘플수 계산을 수행하며 T/R 비 (ratio) 가 1일 때와 점추정치일 경우를 각각 계산하여 결과를 출력한다. 본 자료로 계산한 AUClast의 개인간 (between subject) CV값은 17.63%, 개인내 (within subject) CV값은 16.92%인 것을 알 수 있고 80% 파워로 계산한 샘플 수는 GMR이 1인 경우 6명, 점추정치인 0.95와 같은 경우 7명이 나오게 된다.

test2x2(NCAResult4BE, "AUClast")$`Sample Size`
##                       True Ratio=1 True Ratio=Point Estimate
## 80% Power Sample Size            6                         7

7.2.5 R 샤이니 앱

shiny-be는 비구획분석과 생물학적동등성 분석을 웹브라우저에서 할 수 있는 응용 소프트웨어로 http://www.pipetapps.com/shiny-be 에서 무료로 서비스 하고 있다.

knitr::include_graphics("images/figure-shiny-be.png")
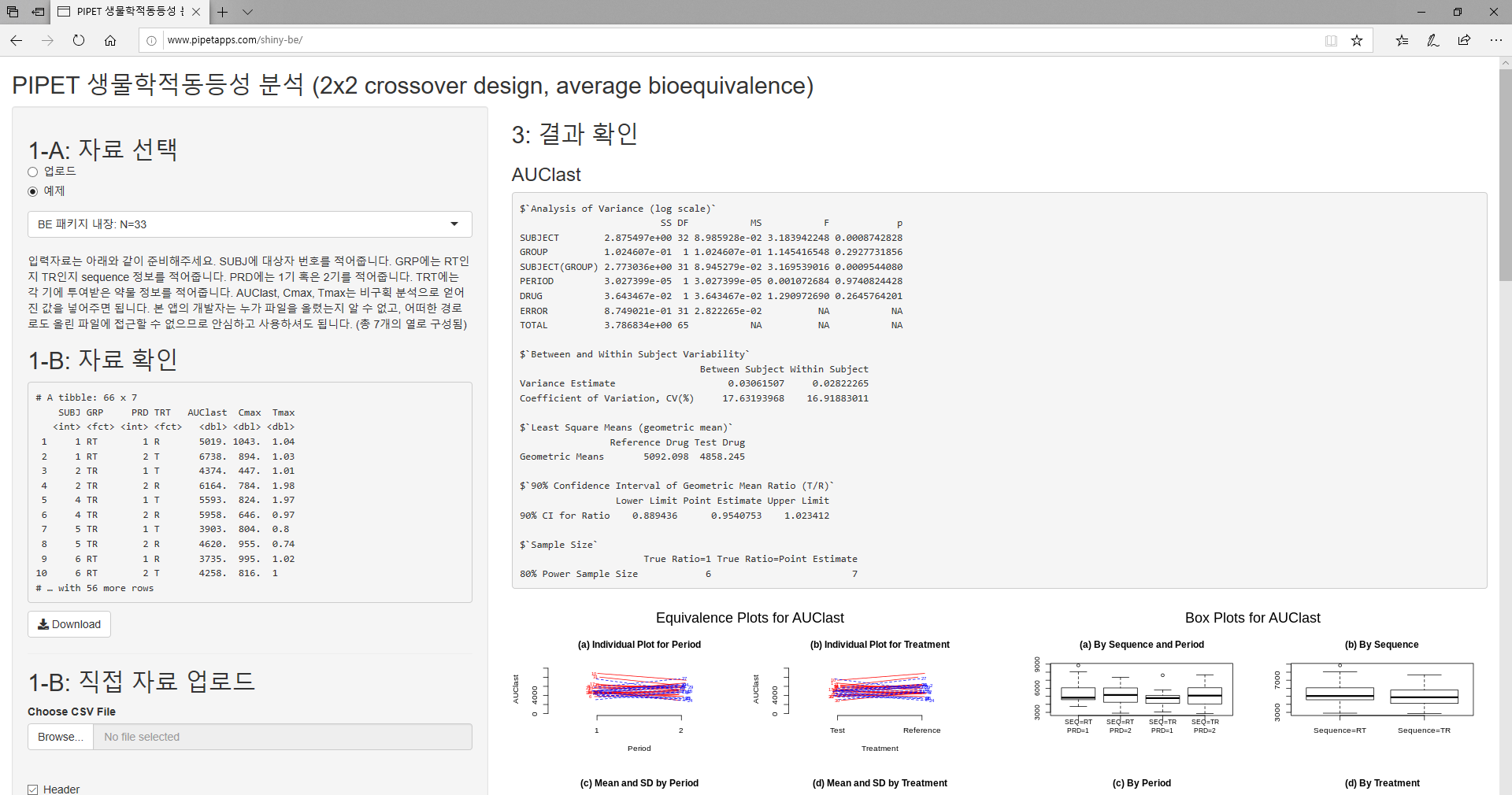
R 샤이니 앱, shiny-be 접속 화면. http://www.pipetapps.com/shiny-be

Figure 7.5: R 샤이니 앱, shiny-be 접속 화면. http://www.pipetapps.com/shiny-be

7.3 논의

knitr::include_graphics("images/figure-traditional-proposed.png")
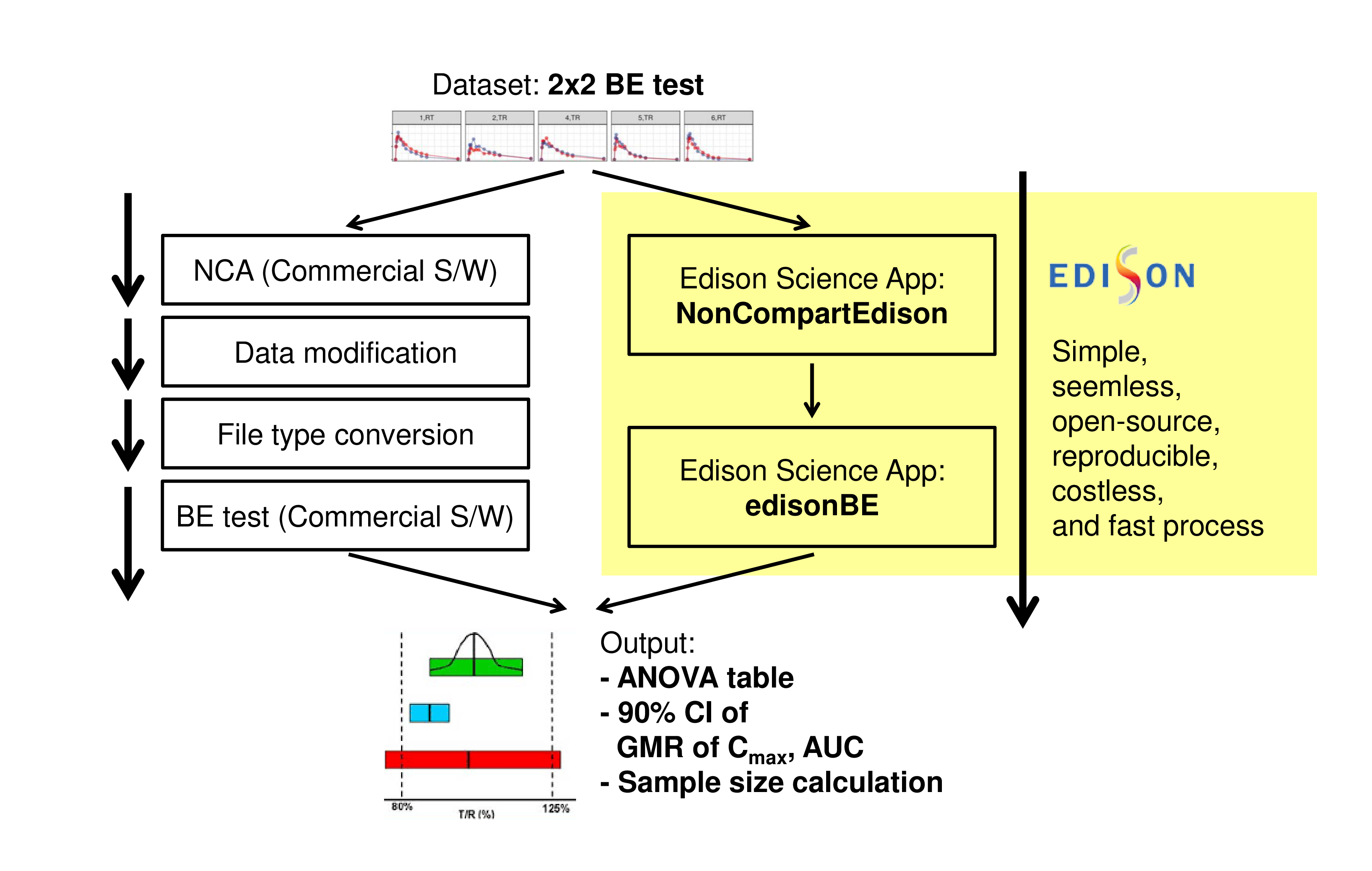
Comparison between a traditional analysis process (left boxes) and the proposed process (right boxes) using EDISON Science Apps.

Figure 7.6: Comparison between a traditional analysis process (left boxes) and the proposed process (right boxes) using EDISON Science Apps.

본 연구는 EDISON 사이언스 앱, R 샤이니 앱을 사용해 쉽고 정확하고 비용이 들지 않는 빠른 비구획분석과 생물학적동등성 분석법을 제시하였다. 현재는 이러한 분석을 위해서 여러 상용 소프트웨어를 필요로 하는 복잡한 단계를 거쳐야 한다. (Figure 3) 따라서 분석 시간이 오래 걸리고 많은 비용이 소모되었다. 본 저자들은 EDISON 사이언스 앱, R 샤이니 앱을 사용하여 이 두 과정을 통합하였고, 이로서 농도-시간 자료로부터 비구획분석과 생물학적동등성 통계 분석까지 연속적으로 가능케 하였다. 본 분석에서 학계와 산업계에서 가장 정확하게 생물학적 동등성을 평가한다고 말하는 SAS통계 패키지와의 비교를 통해 EDISON 사이언스 앱, R 샤이니 앱을 사용한 생물학적 동등성 분석이 정확한 값을 제시함을 검증할 수 있었다. 학생들의 교육에 효과적인 EDISON 사이언스 앱, R 샤이니 앱으로 개발되어 약리학 과목의 필수항목인 약동학의 교육에의 활용도 기대된다. 또한 임상시험 산업계에서도 많은 비용을 절감할 수 있을 것으로 기대된다. 아직은 2x2 교차 설계에서 얻어진 자료로만 분석이 가능하다는 한계를 갖고 있지만 앞으로 다양한 설계를 갖는 자료가 사용 가능하도록 업데이트가 가능할 것이다.

본 연구가 제시하는 EDISON 사이언스 앱, R 샤이니 앱을 통한 방법을 통해 정확한 분석을 빠른 시간에 수행할 수 있을 뿐만 아니라 오류를 줄이고 비용을 절감하는 효과를 가져올 수 있다.

7.4 sasLM

요약

일반 선형 모형 (GLM)은 종속 변수를 독립 변수와 오류 항의 선형 조합으로 설명합니다. SAS ® 의 GLM 절차 와 R의 “car”패키지는 유형 I, II 또는 III ANOVA (분산 분석) 테이블을 계산합니다. 이 연구에서는 SAS ® 의 GLM 절차와 호환되는 새로 개발 된 R 패키지“sasLM”을 검증했습니다 . “sasLM”패키지는 통계 프로그래밍을위한 현재의 골드 표준 인 SAS ® 와 출력을 비교하여 검증되었습니다 . 10 권의 책과 기사의 데이터가 유효성 검사에 사용되었습니다. “sasLM”및 “car”패키지의 결과는 194 모델을 사용하여 SAS ® 의 결과와 비교되었습니다 . “sasLM”의 모든 결과는 SAS ® 의 결과와 동일합니다“car”의 20 개가 넘는 모델이 SAS ® 와 다른 결과를 나타 냈습니다 . “sasLM”패키지의 결과는 SAS ® PROC GLM 의 결과와 유사하기 때문에 “sasLM”패키지는 유형 II 및 III 제곱합을 계산하기위한 대체 방법이 될 수 있습니다. 새로 개발 된 “sasLM”패키지는 무료이며 오픈 소스이므로 다른 유용한 패키지도 개발할 수 있습니다. 우리는“sasLM”패키지가 연구원들이 선형 모델을 편리하게 분석 할 수 있기를 희망합니다.

키워드 :선형 모형 ; 통계 ; 분산 분석 ; 소프트웨어 검증 ; 생물학적 동등성 이동 : 소개 SAS PROC GLM은 “일반 선형 모델”을 나타냅니다. 그러나 많은 통계 학자들은이 용어를 사용하여 “일반화 된 선형 모형”을 나타냅니다. SAS PROC GLM은 다소 오래된 것으로 간주되어 추가 지원이 필요하지 않지만 SAS PROC GLM은 여전히 ​​통계에서 가장 자주 사용되는 절차 중 하나입니다. GLM은 종속 변수를 독립 변수와 오류 항의 선형 조합으로 설명합니다.1 ] 3 가지 선형 모형 : 분산 분석 (ANOVA), 공분산 분석 (ANCOVA), 단순 및 다중 선형 회귀 분석 [2 ]. 분산 분석은 세 개 이상의 알 수없는 모집단 평균 값이 다를 가능성이 있는지 확인하는 데 사용됩니다. 단순 회귀는 직선을 사용하여 두 변수 사이의 관계를 설정하고 다중 회귀는 여러 연속 독립 변수를 사용하여 종속 변수를 설명합니다.3 ]. ANCOVA는 분산 분석과 회귀 분석을 결합한 방법입니다. GLM이 자주 사용되는 이유 중 하나는 실험, 준 실험적 및 비 실험적 데이터에 사용하기 위해 회귀 및 ANOVA가 적용되기 때문에 다양한 유형의 연구 설계에 적합하다는 것입니다.4 ].

분산 분석에서는 가설 검정에 제곱합 (SS)이 사용됩니다. SAS PROC GLM은 4 가지 유형의 SS를 제공합니다.

유형 1 SS : 순차적 SS는 모형에 표시된 항의 순서대로 계산됩니다.

유형 II SS : 우선 순위가 낮은 항의 SS는 동일한 순서로 항을 조정하여 계산 된 다음, 상위 순서의 SS는 동일한 순서로 항을 조절하여 계산됩니다.

유형 III SS : SS는 모든 항 (상호 작용 / 중첩 항 포함)을 동시에 조정하여 계산됩니다.

유형 IV SS : 누락 된 셀이 존재하면 셀의 무게가 추가로 조정됩니다.

SAS PROC GLM은 선형 모델에 대한 절차의 조합 인 PROC REG, PROC ANOVA, PROC TTEST 등으로 간주 될 수 있습니다. 범주 형 변수와 연속 형 변수를 독립 및 종속 변수로 처리 할 수 ​​있습니다. 주요 추정 방법은 ’최대 우도 추정’이 아닌 ’최소 제곱 법’입니다.5 ]. 선형 모델 만 처리하며 선형 모델에는 매개 변수 및 해당 표준 오류에 대한 분석 솔루션이 있습니다. 따라서 ’최소화 알고리즘’이나 반복을 사용하지 않습니다. 오류는 항상 정규 분포로 간주됩니다. 정규 분포 이외의 링크 함수 나 지수 패밀리 분포는 처리하지 않습니다. SAS에서 ’일반 선형 모델’을 사용하려는 사람은 PROC GENMOD 또는 PROC CATMOD와 같은 절차를 사용해야합니다. ’일반화 된 선형 모델’은이 기사의 범위 나 “sasLM”패키지에 포함되지 않습니다.

R의 “차”(적용 회귀에 대한 컴패니언) 패키지는 Fox et al. 모델에 대한 유형 II 또는 유형 III ANOVA 테이블 계산6 ]. 타입 I 및 II 제곱합 (SS)은 R 소프트웨어 커뮤니티에서 더 널리 사용됩니다. R의 anova 및 aov 함수에서 구현 된 SS 유형은 순차적 계산 인 유형 I입니다. 다른 유형의 SS의경우“car”패키지의 Anova 기능이 일반적으로 사용되며 유형 인수가 사용됩니다.

전통적으로 SAS GLM (또는 ANOVA)은 생물학적 동등성 연구 분석에 사용됩니다. 그러나“car”패키지를 사용할 때는 불가능합니다. 따라서“sasLM”패키지 개발에 대한 우리의 초기 동기는 R의 다음 진술을 사용하여 생물학적 동등성 데이터를 처리하는 것이 었습니다.

GLM (log (AUClast) ~ 시퀀스 / 대상 + 기간 + 치료, 데이터 = BEdata)

2 × 2, 6 × 3, 4 × 4와 같은 다양한 크로스 오버 설계에 관계없이 위의 공식을 사용할 수 있다면 매우 편리합니다.

이 연구에서는 SAS ® 의 GLM 절차와 호환되는 새로 개발 된 R 패키지“sasLM”을 검증했습니다 . 은 “sasLM”패키지는 가입자 단말기뿐만 아니라 SAS 구현하기 위해 만들어졌습니다 ® R에, 무료 소프트웨어입니다. 10 권의 책과 기사의 데이터가 유효성 검사에 사용되었습니다.7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ,16 ].

이동 : 행동 양식 소프트웨어를 검증하기위한 화이트 박스 테스트 및 블랙 박스 테스트와 같은 방법을 사용할 수 있지만 본 연구 에서는 골드 표준 (SAS ® ) 과의 비교 가 적용되었습니다.

• 검증 데이터 셋

유효성 검사에 사용 된 데이터 집합에 대한 참조는 다음과 같습니다. 책과 기사에 사용 된 데이터 세트 수는 괄호 안에 표시됩니다.

① 하비 WR. 서브 클래스 수가 같지 않은 데이터의 최소 제곱 분석 : 미국 농무부 농업 연구 서비스; 1960. (3 개의 데이터 세트)

② 재채기 분산 분석에서 예상 평균 제곱의 계산 및 사용. 품질 기술 저널. 1974; 6 (3) : 128-37. (1 데이터 세트)

③ Goodnight JH, 편집자. 새로운 일반 선형 모형 절차. 제 1 차 연례 SAS 사용자 그룹 국제 회의 절차; 1976 : 노스 캐롤라이나 주 SAS Institute Cary. (4 개의 데이터 세트)

④ Littell RC, Stroup WW, Freund RJ. 선형 모델 용 SAS : SAS Institute; 2002. (26 데이터 세트)

⑤ Ojeda MM Sahai H. 랜덤 모델에 대한 분산 분석, 제 2 권 : 불균형 데이터 : 이론, 방법, 응용 및 데이터 분석 : Springer Science & Business Media; 2004. (6 개 데이터 세트)

⑥ Federer WT, King F. 분할 도표 및 분할 블록 실험 설계의 변형 : John Wiley & Sons; 2007. (22 개 데이터 세트)

⑦ Hinkelmann K, Kempthorne O. 실험 설계 및 분석 제 1 권 실험 설계 소개. 2e. John Wiley & Sons Inc. 2008. (21 데이터 세트)

⑧ Hinkelmann K, Kempthorne O. 실험 설계 및 분석 2 권 고급 실험 설계. John Wiley & Sons Inc. 2005. (18 개 데이터 세트)

⑨ Lawson J. SAS 실험 설계 및 분석 : CRC Press; 2010. (33 개 데이터 세트)

r Searle SR, Gruber MH. 선형 모델 : John Wiley & Sons; 2016. (2 개의 데이터 세트)

•“sasLM”패키지

일반 선형 모델을위한 “sasLM”패키지는 무료 공개 사용을 위해 오픈 소스 R 프로그래밍 언어 (버전 3.6.3)로 개발되었습니다. “sasLM”(버전 0.1.4) 패키지는 다음 스크립트를 사용하여 설치 및로드 할 수 있습니다.

자세한 문서와 예제는 CRAN 저장소에 온라인 사용자 설명서에있는 ( HTTP : //CRAN.R- project.org/package=sasLM ), 또한 R 콘솔에서 사용하여 검색 할 수 있습니다 “sasLM을?”.

“sasLM”패키지는 다음 스크립트를 작성하여 사용할 수 있습니다.

•“자동차”패키지

“car”패키지는 다음 스크립트 ( “car”버전 3.0.7)를 작성하여 사용할 수 있습니다.

• SAS ® 소프트웨어

SAS ® 버전 9.4 (SAS Institute Inc., 미국 노스 캐롤라이나 주 캐리) 의 GLM 절차를 사용하여 Type I, II 및 III SS를 얻었습니다. SAS 코드는 다음과 같습니다.

이동 : 결과 “sasLM”, SAS ® 및 “car”패키지 의 결과는 194 모델을 사용하여 비교되었습니다. “sasLM”의 모든 결과 SAS와 동일한 결과를 보였다 ® 은 “자동차”패키지의 20 개 이상의 모델 SAS과 다른 결과를 나타내었다 반면 ® ( 표 1 , 보완 데이터 1 ).은 “자동차”패키지 다른했다 다음 모델 의 “sasLM”패키지 또는 SAS ® 출력 : Snee RD의 기사에서 1 모델 (모델 6) [Goodnight JH의 프레젠테이션에서 8 ], 1 모델 (모델 16) [9 ], Littell RC의 책에서 3 가지 모델 (모델 54, 58, 59) [10 ], Sahai H의 저서 2 모델 (모델 66, 67) [11 ], Federer WT의 책에서 10 모델 (모델 73, 76, 78, 83, 84, 85, 87, 88, 90, 91) [12 ], Hinkelmann K의 저서 1 모델 (모델 118) [13 ] 및 Searle SR의 책에있는 2 가지 모델 (모델 193, 194) [16 ]. 모델 번호는 보충 데이터 1에 표시된 것과 동일합니다.

표 1 SAS ® 와 비교 한 “sasLM”및 “car”패키지의 결과 큰 이미지를 보려면 클릭하십시오 전체 표를 보려면 클릭하십시오 Excel 파일로 다운로드

“sasLM”, SAS ® 및 “car” 에서 동일한 결과를 나타내는 한 데이터 세트 는 “Searle SR, Gruber MHJ, Linear Models 2e, Kindle Edition, John Wiley & Sons Inc, 2016”에 있습니다. 예 3 "[16 ]. 결과는 다음과 같습니다.

• “sasLM”출력

•“자동차”출력

• SAS ® 출력

“sasLM”와 SAS에서 동일한 결과를 보였다 하나 개의 데이터 세트 ® 하지만 “자동차”의 “는 Searle은의 SR, 그루버 MH, 선형 모델 (2E), 킨 판, 존 와일리 & 선즈 사, 2016, 페이지 390”에 있었다 [16 ]. 모델에 별명이 붙은 계수가 있기 때문에“차”결과는 다른 결과와 다릅니다. 결과는 다음과 같습니다.

• “sasLM”출력

•“자동차”출력

• SAS ®

이동 : 토론 선형 모델 분석을 위해 R 용 “sasLM”패키지를 개발했습니다. 유형 I, II 및 III SS는 “sasLM”을 SAS ® 와 동일한 방식으로 사용하여 얻을 수 있습니다 . 이 패키지의 결과는 SAS ® PROC GLM (또는 ANOVA 또는 REG)과 동일하므로 “sasLM”은 SS를 계산하기위한 대체 방법이 될 수 있습니다.

출력간에 약간의 차이가있을 수 있습니다 (마지막 숫자에서 1 씩 꺼짐). 이는 “sasLM”을 포함한 모든 R 패키지에 영향을 미치는 R 반올림 함수의 1에서 1까지의 숫자 방식에서 비롯됩니다. Type II SS와 달리 Type III SS는 1 차 1 차 효과와의 상호 작용 효과를 동시에 조정합니다. 경우에 따라 유형 I 또는 II SS가 유형 III SS보다 선호되지만 [17 ]에서 III 형 SS는 수요가 많지만 R에서는 이용할 수 없었다.

일부 유효성 검사 데이터 집합에서 “sasLM”과 “car”의 차이에 대한 몇 가지 이유가 있습니다. 내포 설계 또는 분할 플롯 설계에서 내포 또는 전체 플롯 계수에 대한 SS는 “자동차”패키지로 계산되지 않습니다. 잔차 자유도가 0 인 경우 “car”는 출력을 생성하지 않습니다. 앨리어싱 계수가있는 경우 “car”패키지는 모델 비교 방법으로 SS를 계산하는 반면 SAS는 g2 일반화 역을 사용하여 SS를 계산합니다.9 ,10 ].

“sasLM”을 사용하여 생물학적 동등성 데이터를 분석 할 수도 있지만, 현재 의견으로는 선형 혼합 효과 모델 (예 : PROC MIXED, nlme)에 원래 사용 된 도구가 원래 고정 효과 모델 (예 : PROC MIXED, nlme)에 적합합니다. , GLM, ANOVA, sasLM). 이러한 단점에도 불구하고, 고정 효과를 사용하는 실험의 설계는 여전히 무한합니다. 따라서“sasLM”패키지는 많은 경우에 유용 할 수 있다고 생각합니다.

은 “sasLM”패키지로 SAS 모델 출력과 비교하여 확인 하였다 ® 통계 프로그램의 현재 금 표준 SAS 때문에 PROC GLM을 ® . 올바른 제품이 구축되고 있는지 확인하기 위해 소프트웨어 유효성 검사가 수행됩니다. 이 소프트웨어는 공급시 소프트웨어가 의도 한 용도를 충족하는지 확인하기위한 역동적 인 테스트 프로세스입니다. 소프트웨어를 검증하는 방법은 여러 가지가 있지만 [17 ,18 ], 우리는 현재 금 표준과 비교하는 것이 가장 좋다고 생각했습니다.19 ].

새로 개발 된 “sasLM”패키지는 무료이며 오픈 소스이므로 다른 유용한 패키지도 개발할 수 있습니다. 우리는“sasLM”패키지가 연구원들이 선형 모델을 편리하게 분석 할 수 있기를 희망합니다.

  1. 식품의약품안전청 식. 동등생물의약품 평가 가이드라인. 2009.
  2. Chow S-C, Liu J-p. Design and analysis of bioavailability and bioequivalence studies. Chapman & Hall/CRC biostatistics series, vol 27, 3rd edn. CRC Press, Boca Raton, 2009
  3. Yoon S-H, Hwang N-A, Lim Y-C, Lee Y-B, Park J-S. Development of BioEquiv, a Computer Program for the Analysis of Bioequivalence. Journal of Korean Pharmaceutical Sciences 2010;40:1-7. doi: 10.4333/kps.2010.40.1.001.
  4. R Core Team, R Foundation for Statistical Computing. R: A Language and Environment for Statistical Computing. https://www.R-project.org/ 2018

참고문헌

Bae, Kyun-Seop. 2018. BE: Bioequivalence Study Data Analysis. https://CRAN.R-project.org/package=BE.

Chow, S. C., and J. Liu. 2008. Design and Analysis of Bioavailability and Bioequivalence Studies. Chapman & Hall/Crc Biostatistics Series. CRC Press. https://books.google.co.kr/books?id=KtKJFGJeV3MC.