Get Lambdas and Coefficients of Three-compartment Model

It calculates lambdas and coefficients for three-compartment model from K10, K12, K21, K13, and K31.

SolComp3(K10, K12, K21, K13, K31)

Arguments

K10	Ke, Elimination rate constant from central compartment
K12	Rate constant from the central to the first peripheral compartment
K21	Rate constant from the first peripheral to the central compartment
K13	Rate constant from the central to the second peripheral compartment
K31	Rate constant from the second peripheral to the central compartment

Details

It calculates lambdas and coefficients of two-compartment model from K10, K12, and K21. Lambdas should have no identical values.

Value

This returns a list of lambdas and coefficients.

Author

Kyun-Seop Bae <k@acr.kr>

Examples

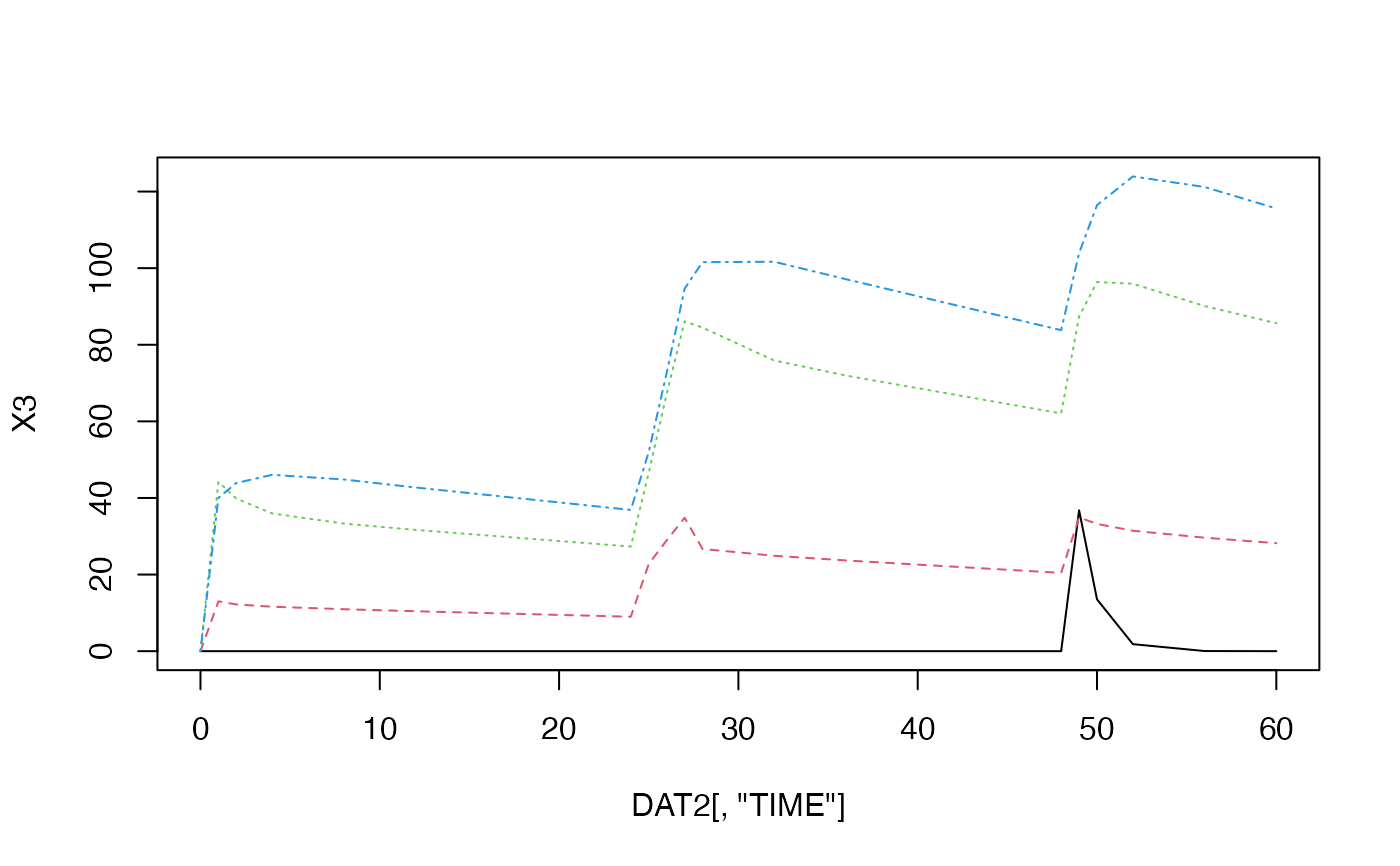
DAT
#>    TIME AMT RATE CMT DV
#> 1     0 100    0   2 NA
#> 2     1  NA   NA  NA NA
#> 3     2  NA   NA  NA NA
#> 4     4  NA   NA  NA NA
#> 5     8  NA   NA  NA NA
#> 6    12  NA   NA  NA NA
#> 7    24 150   50   2 NA
#> 8    25  NA   NA  NA NA
#> 9    26  NA   NA  NA NA
#> 10   28  NA   NA  NA NA
#> 11   32  NA   NA  NA NA
#> 12   36  NA   NA  NA NA
#> 13   48 100    0   1 NA
#> 14   49  NA   NA  NA NA
#> 15   50  NA   NA  NA NA
#> 16   52  NA   NA  NA NA
#> 17   56  NA   NA  NA NA
#> 18   60  NA   NA  NA NA
DAT2 = ExpandDH(DAT)
Sol = SolComp3(K10=0.1, K12=3, K21=1, K13=2, K31=0.5)
X3 = nComp(Sol, Ka=1, DAT2)
X3
#>               [,1]      [,2]     [,3]      [,4]
#>  [1,] 0.000000e+00  0.000000  0.00000   0.00000
#>  [2,] 0.000000e+00 13.004819 44.19187  40.02386
#>  [3,] 0.000000e+00 12.205766 39.85761  43.90691
#>  [4,] 0.000000e+00 11.604779 35.94874  46.04289
#>  [5,] 0.000000e+00 10.954285 33.31609  44.82325
#>  [6,] 0.000000e+00 10.422939 31.66063  42.73598
#>  [7,] 0.000000e+00  8.993606 27.31648  36.88080
#>  [8,] 0.000000e+00 22.781008 46.57865  51.99548
#>  [9,] 0.000000e+00 28.923842 67.17024  72.67283
#> [10,] 0.000000e+00 34.824944 86.10027  94.65280
#> [11,] 0.000000e+00 26.682954 84.48999 101.57568
#> [12,] 0.000000e+00 24.912956 75.89143 101.67155
#> [13,] 0.000000e+00 23.688228 71.96288  97.10912
#> [14,] 0.000000e+00 20.438779 62.07916  83.81492
#> [15,] 3.678794e+01 34.919791 87.37083 103.91654
#> [16,] 1.353353e+01 33.228471 96.38124 116.45056
#> [17,] 1.831564e+00 31.441383 95.92774 123.94904
#> [18,] 3.354626e-02 29.630545 90.10716 121.19273
#> [19,] 6.144212e-04 28.190201 85.63118 115.58182
matplot(DAT2[, "TIME"], X3, type="l")