Chapter 2 이론 및 계산방법
2.1 EDISON 사이언스 앱, R 샤이니 앱과 R 패키지
본 분석에서 사용될 EDISON 사이언스 앱, R 샤이니 앱은 NonCompartEdison, edisonBE 두 종류이다.
비구획분석과 생물학적동등성 통계 분석을 하게 되며 R 기반 [4] 으로 프로그래밍 되어 있다.
각각은 NonCompart와 BE라는 이름의 R 패키지 형태로 공개되어 배포 되고 있다.
R 콘솔에서는 다음을 입력함으로서 각 라이브러리를 불러올 수 있다.
EDISON 사이언스 앱, R 샤이니 앱을 제작하는데 사용한 R 코드 및 자료(datasets)는 https://github.com/asancpt/edison-noncompart, https://github.com/asancpt/edison-BE 에 각각 공개되어 있다.
2.2 모형
\[ Y_{ijk} = \mu + S_{ik} + P_{j} + F_{j,k} + C_{(j-1,k)} + \varepsilon_{ijk} \]
이때에 μ; 전체 평균, Sik; k 번째 sequence에서 i 번째 subject의 효과(랜덤), Pj : j번째 period 의 효과(고정), Fj, k; k 번째 sequence에서 j 번째 period의 제제의 효과(고정), C(j-1,k): k 번째 sequence에서(j-1) 번째 period의 잔류효과(고정), εijk : 오차항으로 정의한다. 이 모델에서 사용하는 가정은 1) Sik ∼ N(0,σs²), 2) εijk ∼ N(0,σe²), 3) Sik 와 εijk가 독립이라는 세가지 이다. 이때 (μT - μR)에 대한 (1-2α)×100% 신뢰구간이 ln(0.8), ln(1.25) 안에 들어가면 두제제가 생물학적으로 동등하다 결론을 내릴 수 있다.
2.3 SAS 코드
SAS는 통계 패키지중에서는 가장 방대하고 다양한 분석을 제공하고 전 세계적으로 생물학적동등성의 판단을 위해 표준으로 사용되고 있다. 다음과 같이 2x2 교차설계 자료를 분석하기 위한 SAS 코드 (PROC GLM, PROC MIXED, SAS version 9.4)를 작성하고 EDISON 사이언스 앱, R 샤이니 앱에서 계산된 결과와 비교하였다.
PROC GLM DATA=BE OUTSTAT=STATRES; /* GLM use only complete subjects. */
CLASS SEQ PRD TRT SUBJ;
MODEL LNAUCL = SEQ SUBJ(SEQ) PRD TRT;
RANDOM SUBJ(SEQ)/TEST;
LSMEANS TRT /PDIFF=CONTROL('R') CL ALPHA=0.1 COV OUT=LSOUT;
PROC MIXED DATA=BE; /* MIXED uses all data. */
CLASS SEQ TRT SUBJ PRD;
MODEL LNAUCL = SEQ PRD TRT;
RANDOM SUBJ(SEQ);
ESTIMATE 'T VS R' TRT -1 1 /CL ALPHA=0.1;
ODS OUTPUT ESTIMATES=ESTIM COVPARMS=COVPAR;2.4 자료의 형태, 자료의 구성요소
2x2 cross-over design이 가장 기본적인 디자인(통상 RT / TR)으로 사용된다. 피험자를 무작위로 두 군으로 나누어 각 군별로 동일 성분의 대조약과 시험약을 각각 투여(제1기 투약)하고 피험자별로 투약 전후 정해진 시간마다 채혈하고 농도 측정한다. 이전에 투여한 약이 모두 배설될 정도로 충분한 기간 경과 (보통 반감기의 5배 이상) 후 각 군별로 대조약과 시험약을 바꾸어 각각 투여하고(제2기 투약) 동일하게 혈액 채취 및 혈중농도 측정하게 된다.
본 논문에서는 위와 같은 시나리오로 시뮬레이션을 통해 얻어진 약동학 파라미터를 사용해 자료가 구성되었고, EDISON 사이언스 앱인 NonCompartEdison에서 입력으로 사용될 자료의 형태는 Table 1와 같다. SEQ (sequence), TRT (treatment), SUBJ (subject), and PRD (period, 기)의 자료가 열 형태로 제시되어야 하며 이는 edisonBE 앱에서 사용되는 약동학 파라미터 자료에도 일종의 primary key로 사용되기 때문에 유사한 형태로 보존되어야 한다. 33명의 대상자의 개인별 농도-시간 그래프는 Figure 1에 나타내었다.
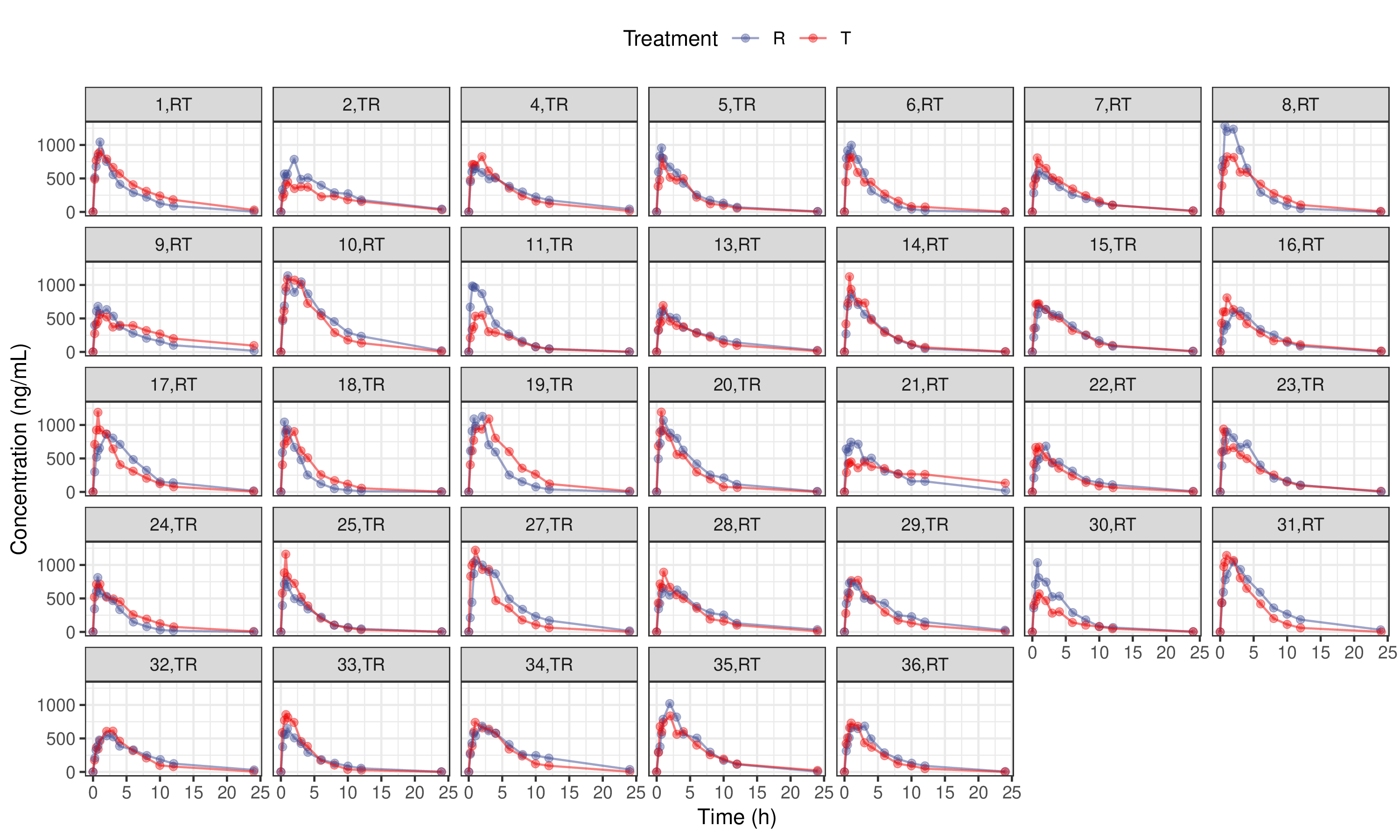
Figure 1. Concentration-time curves of raw data (N=33)